Pick up almost any financial magazine or newspaper and you’ll find full-page ads touting the recent performance of mutual funds and ETFs. What’s the reason for their outperformance? The fund companies will give the credit to the genius of the manager, but there’s a way you can tease out a more complete explanation: it’s called factor analysis.

Don’t worry, I’m not going to get all mathy on you—well, maybe a little bit. Performing this kind of analysis is complicated, but understanding the basic ideas doesn’t require a a Ph.D. in statistics. We know  investment returns come from exposure to known risk factors (or premiums), and every equity portfolio is exposed to these in varying degrees. What we want to learn is how much each factor contributed to the fund’s returns. If the fund outperformed or underperformed its benchmark, factor analysis can tell you why.

Just the factors, ma’am

What are the risk factors? The first is the market premium (or equity premium), which is simply the expected excess return from stocks compared with risk-free investments like T-bills. The second is the value premium: stocks with high book-to-market ratios have historically delivered higher returns than growth stocks. The third is the size premium, which accounts for the higher expected returns of small-cap stocks over large-caps. Together these are known as the Fama-French Three-Factor Model, something I have written about previously.

The analysis works like this. First you collect monthly performance data for each of the three factors and drop them into an Excel spreadsheet. (In the example below, the data come from Andrea Frazzini’s Data Library.) Then you import the monthly returns of the fund you want to examine. Finally you run what’s called a regression analysis, which reveals the relationship between the fund’s returns and those of each factor.

Let’s say over a five-year period value stocks outperformed growth stocks and small caps beat large caps. Running a factor analysis on a celebrated mutual fund might reveal much of the outperformance simply came from the fund’s higher exposure to the value and size premiums. It might also reveal whether unknown factors—which could include the manager’s stock-picking ability—had a positive or negative impact.

Unpacking the jargon

An example will help explain. Let’s look at the results of a factor analysis on the iShares S&P/TSX Capped Composite (XIC), which tracks the broad Canadian equity market. The data cover the five years from 2008 through 2012.

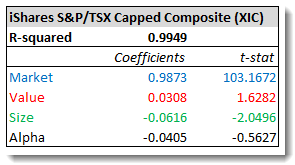XIC factorsOK, let’s unpack all the jargon. The first key number is the R-squared, which tells you how well the data fit the model. In this case, a figure of 0.9949 indicates the three factors we’ve analyzed explain 99.49% of the performance of XIC. It’s an almost perfect fit.

Now look at the numbers in the “Coefficients” column. These numbers measure the relationship between two variables—in this case, the fund’s monthly returns and each of the factors. A coefficient of +1 indicates the variables move in the same direction by the same amount. A value of –1 indicates the variables move in opposite directions, also by the same amount. A value of zero means the variables move independently of one another.

In our example above, the correlation between the monthly returns of XIC and the market factor is very close to 1, which is what you would expect from an index fund tracking the whole market. The close-to-zero figures for the value and size factors indicate these have no meaningful effect on the fund’s performance. During periods when value or small-cap stocks outperform or lag, the effect on XIC would be negligible.

The bottom row, labeled Alpha, is the portion of the fund’s performance that is not explained by the three factors. If an active fund manager added excess returns (or caused some underperformance), that would show up here as a positive number. But so would dumb luck—remember, alpha indicates outperformance or underperformance, but it doesn’t explain what caused it. In the case of an index fund like XIC, you should expect a slightly negative alpha because of the management fee.

The last column (t-stat) helps you determine whether the results are meaningful. As a rule of thumb, a t-stat higher than 2 or lower than –2 indicates the coefficient is statistically significant. A number closer to zero means it could just be noise. In this example, we can see the market and size coefficients are significant, while the value and alpha numbers are less reliable.

I realize all this is rather technical, but bear with me during my next couple of posts, because it’s all heading toward some interesting findings. Later this week I’ll look at two traditional ETFs with added exposure to the value and small-cap factors. Then we’ll look at some other popular Canadian equity ETFs to see what’s driving their performance.

Note: Thanks to Justin Bender of PWL Capital for running these analyses, and to Andrea Frazzini of AQR Capital Management for supplying the data. I’d also like to thank Nathan Stretch, a long-time reader who pointed us to data sources and shared many of his own regression analyses with Justin and me. Nathan is the founder of Search Tempest and AutoTempest, which aggregate classified ads and automotive ads from multiple sources.